First-order logic itu salah satu jenis sistem formal, yang digunakan untuk membuktikan kebenaran dari sebuah pernyataan.
Dalam first-order logic, setiap pernyataan dianggap memiliki predikat. Predikat itu dapat menghubungkan pernyataan yang satu dengan yang lain.
Kalimat-kalimat dalam first-order-logic dibuat dengan format P( X, Y). P adalah predikat dan X adalah subjek. Y adalah objek, yang merupakan variabel yang opsional.
Contoh kalimatnya adalah sebagai berikut:
Kalimat asli: James makan apel.
Kalimat FOL: makan(James, apel)
Kalimat FOL dapat juga diberikan kuantor dan tanda-tanda logika lain, seperti berikut:
Kalimat asli: James suka daging dan Daisy suka sayur.
Kalimat FOL: suka(James, daging) ^ suka(Daisy, sayur)
Pembuktian
Ada dua cara untuk melakukan pembuktian menggunakan FOL, yaitu backward chaining dan proof by resolution.
Untuk lebih jelasnya, langsung saja dijelaskan melalui contoh soal.
Misalkan ada kalimat-kalimat berikut:
- Thomas adalah seorang raja Inggris.
- Tina tinggal di kerajaan Inggris.
- Semua orang yang tinggal di kerajaan bahagia ketika raja baik.
- Thomas baik.
Lalu ditanyakan apakah Tina bahagia.
Pertama-tama, dibuat dulu bentuk FOL-nya, yaitu seperti berikut:
- Raja(Thomas, Inggris)
- Tinggal(Tina, Inggris)
- ∀X, ∃Y, ∃Z: Tinggal(X, Y) ^ Raja(Z, Y) ^ Baik(Z) -> Bahagia(X)
- Baik(Thomas)
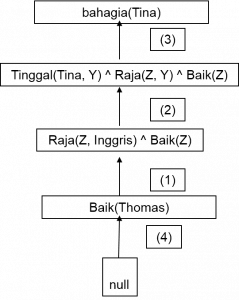
1. Cara backward chaining
Pada backward chaining, kita memulai pengecekan dengan menggunakan pertanyaan tadi sebagai awal chain. Lalu dilakukan chaining dengan premis-premis lain hingga menghasilkan nilai null.
Hasilnya adalah sebagai berikut:
2. Cara proof by resolution
Proof by resolution menggunakan teknik kontradiksi, dimana kita menggunakan premis yang berlawanan nilainya untuk membuktikan sesuatu.
Untuk melakukan proof by resolution, semua premis harus dibuat menjadi clause normal form (CNF) terlebih dahulu. Dalam CNF, semua premis tidak boleh menggunakan kuantor, implikasi (jika X maka Y) dan biimplikasi (X jika dan hanya jika Y). Lalu, jawaban dari pertanyaan dianggap salah dan dijadikan premis. Premis baru ini dijadikan awal dari pembuktian.
CNF dari premis-premis tadi adalah sebagai berikut:
- Raja(Thomas, Inggris)
- Tinggal(Tina, Inggris)
- ~Tinggal(X1, Y1) v ~Raja(Z1, Y1) v ~Baik(Z1) v Bahagia(X1)
- Baik(Thomas)
- ~Bahagia(Tina)
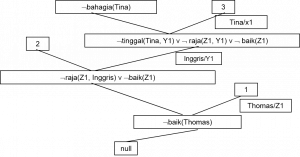
Selanjutnya cara pengerjaan mirip dengan backward chaining, tetapi yang dihubungkan adalah premis dengan hasil yang berlawanan. Hasil kerjanya adalah sebagai berikut: